A few days back I had the chance to talk to Niraj, the guy behind most of the HSolve related code in MOOSE. He ran through the entire math behind HSolve and I thought I should put that down here as it will help clear many of the doubts that you may be having. Let's start with the current equation for one compartment:
Now, out of these variables, some of them vary with time, while others stay constant. Let's take some time t=1. We will denote the time varying variables with a suffix 1. Then the equation for the ith compartment becomes:
Let us keep that equation aside for a moment and look at another bit of the derivation - The backward Euler method of approximation.
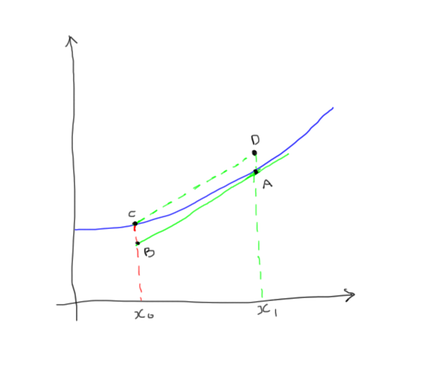
Understanding how this approximation is done is very simple with a diagram.
Understanding how this approximation is done is very simple with a diagram.
This is a (very) rough diagram to show how the approximation works. The blue line is a plot of some function F(n). Let's take two points on the X-axis, X0 and X1. We mark their locations on the plot as points C and A. Now, we take the slope of the function at A (given by the solid green line) and extend it back to the vertical line from X0. We then draw a line parallel to the just drawn line, starting from C and hitting the vertical line from X1. This is an approximation of the function at point X1 given it's value at X0 and it's slope at X1. This would predict the value of the function at X1 to be D, whereas the actual value is A.
This is how future values of the Voltages and Admittances are predicted in MOOSE.
So the equation used when performing Backward Euler Approximations is:
This is how future values of the Voltages and Admittances are predicted in MOOSE.
So the equation used when performing Backward Euler Approximations is:
Now, we just replace dV/dt with the equation we got above. Remember that the C term which was on the Left Hand Side is brought down to the denominator of the RHS before substitution. That will give:
Taking all the V1 terms together, we get
We shift that last term to the LHS and take V1 out common to get
This can be simplified as follows by making the following substitutions
Where
So these coefficients you see are what actually goes into the Hines matrix. Aii are the diagonal terms, Aij are the off diagonal terms and Bi are the terms in the B matrix.
Hopefully, this will make the math behind HSolve a little more clear. It certainly helped me understand what was really going on.
Hopefully, this will make the math behind HSolve a little more clear. It certainly helped me understand what was really going on.
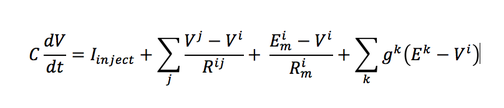
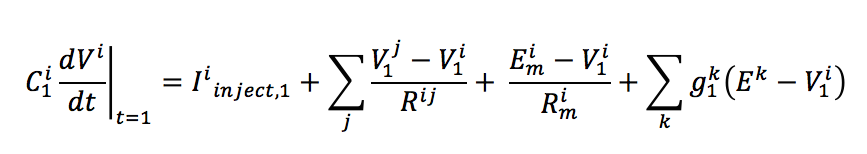
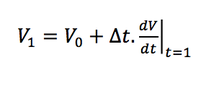
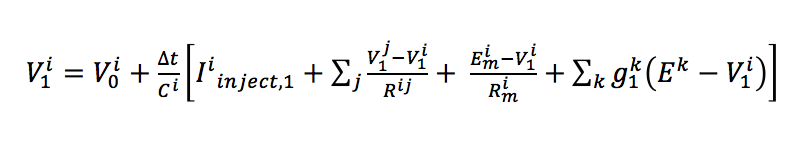
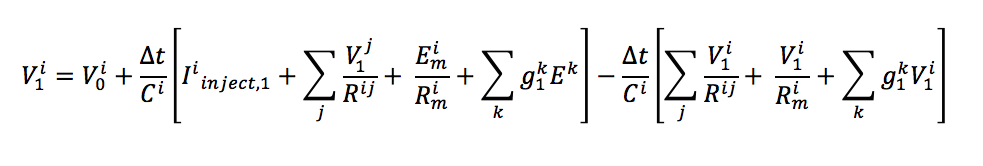
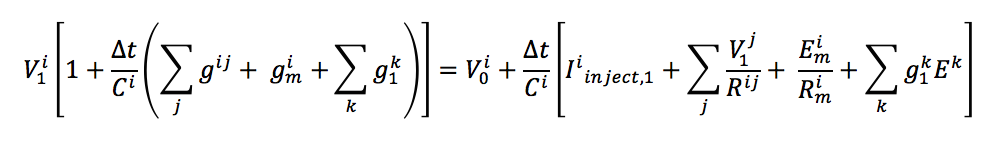
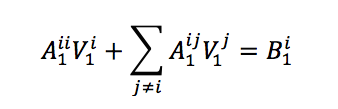
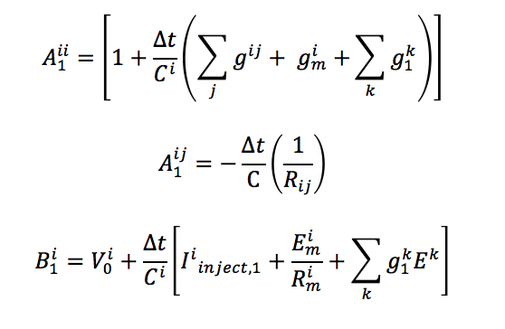
 RSS Feed
RSS Feed
