"MOOSE is the Multiscale Object-Oriented Simulation Environment. It is the base and numerical core for large, detailed simulations including Computational Neuroscience and Systems Biology."
This is the definition of MOOSE given by its creators. It basically provides a framework using which biological systems can be easily modelled and simulated, with comparatively less work from the programmer (than starting the programming from scratch).
The project is hosted at sourceforge here: http://moose.sourceforge.net/
A lot of the information on this page (most of it in fact) is derived from the work of James M Bower and David Beeman in The Book of Genesis. Here, I have merely picked the parts of the book that are most relevant to my work and presented it. In order to gain an in depth understanding of this field, I would suggest reading up the original book.
This is the definition of MOOSE given by its creators. It basically provides a framework using which biological systems can be easily modelled and simulated, with comparatively less work from the programmer (than starting the programming from scratch).
The project is hosted at sourceforge here: http://moose.sourceforge.net/
A lot of the information on this page (most of it in fact) is derived from the work of James M Bower and David Beeman in The Book of Genesis. Here, I have merely picked the parts of the book that are most relevant to my work and presented it. In order to gain an in depth understanding of this field, I would suggest reading up the original book.
Introduction
Neurons work on the basis of exchanging currents between them through synaptic connections. This current exchange happens by virtue of fluctuating potentials within each neuron, caused by a number of chemical and electrical processes within it. Thus, in order to simulate all the processes taking place inside a collection of neuron and simulate it accurately, its electrical properties must be accurately understood and simulated.
The electrical properties of a neuron are not constant throughout its structure. It varies with space and time. Thus, in order to simulate it, two methods can be used:
Neurons work on the basis of exchanging currents between them through synaptic connections. This current exchange happens by virtue of fluctuating potentials within each neuron, caused by a number of chemical and electrical processes within it. Thus, in order to simulate all the processes taking place inside a collection of neuron and simulate it accurately, its electrical properties must be accurately understood and simulated.
The electrical properties of a neuron are not constant throughout its structure. It varies with space and time. Thus, in order to simulate it, two methods can be used:
- A complex function can be formulated that defines its electrical properties at every point, and also specifies the way this varies over time.
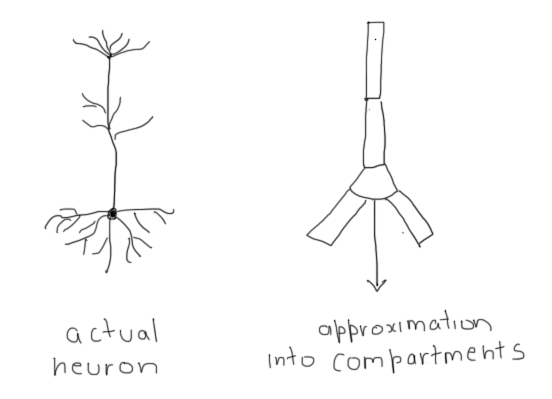
- The neuron can be broken up into smaller compartments, each of which will have constant properties, but will interact with each other in order to represent the whole neuron together.
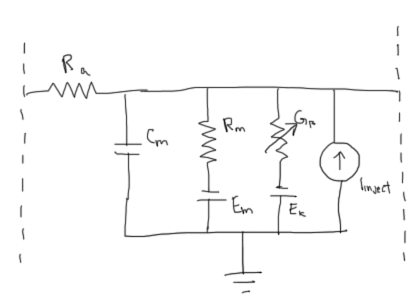
The electrical properties of the compartments can be approximated to the following electrical circuit:
The area inside the dotted lines is one compartment. This will be connected to other compartments on one or both sides. Here is a brief description of the different components of the circuit:
- Ra is the axial resistance. That is, the resistance that will be encountered as current enters the compartment.
- Cm is the capacitance offered by the cell membrane. This happens because the membrane itself is an insulator of current, and there is a potential difference between the inside and outside of the neuron.
- Rm and Em are the membrane resistance and membrane potential respectively, and are caused by the passive ion channels in the neuron.
- Gk is the conductance caused by the active ion channels in the neuron. This is expected to change dynamically during a simulation. Hence the variable resistor in its depiction. Ek is the associated potential, called Equilibrium Potential
- Iinject is the sudden current flow caused by firing of action potentials or provided by inserting of an electrode into the compartment.
This equation depends on Vm’ and Vm’’ which are the potentials of the two neighboring compartments. These compartments have their own equations for their potentials which will depend on their neighbors and so on. Thus, all these coupled equations must be solved in parallel.
Solving for Vm using this equation at every compartment in the neuron, and further for every neuron, will give the required prediction of the state of the model at the next time step. This is the ultimate goal of MOOSE.
This is done by creating a difference equation and solving for this using one of mutliple methods. The default is the Exponential Euler (EE) method. Other methods are the Backward Euler and Crank-Nicholson Methods, which are faster to compute, but require more work in order to set up correctly.
Solving for Vm using this equation at every compartment in the neuron, and further for every neuron, will give the required prediction of the state of the model at the next time step. This is the ultimate goal of MOOSE.
This is done by creating a difference equation and solving for this using one of mutliple methods. The default is the Exponential Euler (EE) method. Other methods are the Backward Euler and Crank-Nicholson Methods, which are faster to compute, but require more work in order to set up correctly.
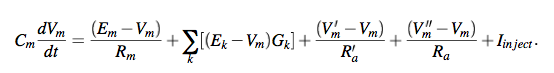
 RSS Feed
RSS Feed
